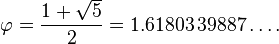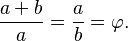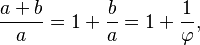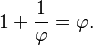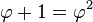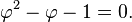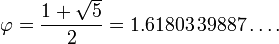Penjelasan: barisan ini berawal dari 0 dan 1, kemudian angka berikutnya didapat dengan cara menambahkan kedua bilangan yang berurutan sebelumnya. Dengan aturan ini, maka barisan bilangan Fibonaccci yang pertama adalah:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946...

Barisan bilangan Fibonacci dapat dinyatakan sebagai berikut:

F_n = (x₁ⁿ – x₂ⁿ)/ sqrt(5)

dengan

F_n adalah bilangan Fibonacci ke-n
x₁ dan x₂ adalah penyelesaian persamaan x² – x – 1 = 0.

Perbandingan antara F_n+1 dengan F_n hampir selalu sama untuk sebarang nilai n dan mulai nilai n tertentu, perbandingan ini nilainya tetap. Perbandingan itu disebut rasio emas yang nilainya mendekati 1,618.

Golden Ratio

12/11/2013 06:18

Rasio emas

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas

(Dialihkan dari Golden ratio)

Ini adalah versi yang telah diperiksa dari halaman ini

Langsung ke: navigasi, cari

Ruas garis dalam rasio emas

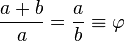Sebuah persegi panjang emas dengan sisi panjang a dan sisi pendek b, jika diletakkan berhimpitan dengan bujur sangkar dengan panjang sisi a, maka akan menghasilkan kemiripan persegi emas dengan sisi panjang a + b dan sisi pendek a. Hal ini dirumuskan melalui persamaan matematika $\frac{a+b}{a} = \frac{a}{b} \equiv \varphi$ .

Cara menggambar sebuah persegi panjang emas:
1. Buatlah gambar sebuah bujur sangkar/persegi (merah).
2. Tarik satu garis memotong tepat di tengah persegi membaginya menjadi 2 bagian.
3. Tarik garis dari titik perpotongan garis tengah dengan sisi persegi ke sudut persegi (panah abu-abu), jadikan ini sebagai jari-jari lingkaran.
4. Dengan menggunakan jangka buatlah satu lingkaran dengan pusat di titik perpotongan sesuai jari-jari, lingkaran menyentuh dua sudut persegi.
5. Tarik satu garis baru sesuai sisi persegi hingga berpotongan dengan lingkaran, buat persegi panjang baru berdasarkan titik pertemuan sisi-sisi ini (biru). Gabungan persegi dengan persegi panjang membentuk persegi panjang emas.

Dalam matematika dan seni, dua nilai dianggap berada dalam hubungan rasio emas ( $\varphi$ ) jika rasio antara jumlah kedua nilai itu terhadap nilai yang besar sama dengan rasio antara nilai besar terhadap nilai kecil. Nilai yang lebih besar dilambangkan dengan huruf a, sedangkan nilai yang lebih kecil dilambangkan dengan huruf b. Gambar di sebelah kanan menggambarkan hubungan geometrik yang jika dirumuskan secara aljabar adalah sebagai berikut:

$\frac{a+b}{a} = \frac{a}{b} \equiv \varphi,$

dimana huruf Yunani phi ( $\varphi$ ) mewakili rasio emas. Nilainya adalah:

$\varphi = \frac{1+\sqrt{5}}{2} = 1.61803\,39887\ldots.$

^[1]

Setidaknya sejak Abad Renaisans, banyak seniman dan arsitek telah membuat proporsi karya sesuai dengan rasio emas—terutama dalam bentuk persegi emas, yaitu perbandingan sisi panjang terhadap sisi pendek sesuai dengan nilai rasio emas—dipercaya proporsi ini secara estetika sangat ideal. Sebuah persegi panjang emas dapat dipotong menjadi persegi dan persegi panjang kecil dengan rasio aspek yang sama persis. Para ahli matematika sejak zaman Euclid telah mempelajari rasio emas karena sifatnya yang unik dan menarik. Rasio emas juga digunakan dalam analisis pasar keuangan, serta strategi seperti retraksi Fibonacci.

Rasio emas sering kali disebut bagian emas (Latin: sectio aurea) atau rata-rata emas.^[2]^[3]^[4] Nama lainnya antara lain rasio ekstrem dan rata-rata,^[5] bagian tengah, proporsi ilahiah, bagian ilahiah (Latin: sectio divina), proporsi emas, potongan emas,^[6] angka emas, dan rata-rata Phidias.^[7]^[8]^[9]

Daftar isi

Perhitungan

Templat:Bilangan irasional
Biner	1.1001111000110111011...
Desimal	1.6180339887498948482...
Heksadesimal	1.9E3779B97F4A7C15F39...
Pembagian berkelanjutan	$1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}}$
Bentuk aljabar	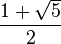$\frac{1 + \sqrt{5}}{2}$
Seri infinit	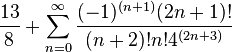$\frac{13}{8}+\sum_{n=0}^{\infty}\frac{(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}$

Dua nilai a dan b dinyatakan berada dalam hubungan rasio emas φ jika:

$\frac{a+b}{a} = \frac{a}{b} = \varphi.$

Salah satu cara untuk menemukan nilai φ adalah dengan memulai pembagian sisa. Dengan cara menyederhanakan pembilang dan penyebutnya dalam b/a = 1/φ,

$\frac{a+b}{a} = 1 + \frac{b}{a} = 1 + \frac{1}{\varphi},$

hal ini menunjukkan

$1 + \frac{1}{\varphi} = \varphi.$

Dikalikan dengan φ menghasilkan

$\varphi + 1 = \varphi^2$

yang dapat diatur menjadi

${\varphi}^2 - \varphi - 1 = 0.$

Dengan menggunakan formula kuadrat menghasilkan jawaban positif yaitu

$\varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\,39887\dots.$

Sejarah

Ahli matematika Mark Barr mengusulkan menggunakan huruf pertama nama seorang pematung Yunani Phidias, phi, untuk melambangkan rasio emas. Biasanya digunakan huruf kecil (φ). Kadang-kadang huruf besar (Φ) idigunakan dalam resiprokal rasio emas, 1/φ.

Rasio emas telah memikat kaum intelektual barat dari berbagai latar belakang disiplin ilmu selama sekurangnya 2.400 tahun. Menurut Mario Livio:

Sekian banyak cendekiawan matematika dari berbagai era, seperti Pythagoras dan Euclid dari Yunani kuno, sampai ahli matematika Italia abad pertengahan Leonardo da Pisa dan ahli astronomi Renaissance Johannes Kepler, hingga tokoh-tokoh ilmuwan seperti pakar fisika dari Oxford Roger Penrose, telah menghabiskan banyak waktu untuk memahami rasio sederhana ini dengan sifat-sifatnya. Akan tetapi ketakjuban akan rasio emas ini tidak hanya terbatas di kalangan ahli matematika saja. Ahli biologi, seniman, musisi, sejarawan, arsitek, psikolog, dan bahkan ahli mistik telah berdebat mengenai hakikat keserbaadaannya dan daya tariknya. Bahkan, mungkin patut dikatakan bahwa rasio emas telah mengilhami begitu banyak pemikir dari berbagai disiplin ilmu dibandingkan angka apapun dalam sejarah matematika.^[10]

Ahli matematika Yunani kuno pertama kali mempelajari hal yang kini dikenal sebagai rasio emas karena kerap muncul dalam geometri. Pembagian garis menjadi "rasio ekstrem dan rata-rata" (bagian emas) sangat penting dalam geometri pentagram dan pentagon. Bangsa Yunani biasanya mengaitkan penemuan konsep ini dengan Pythagoras atau pengikutnya. Pentragram yang dibubuhi pentagon menjadi lambang kaum pendukung paham Pythagoras.

Elemen Euclid (Yunani: Στοιχεῖα) memberikan definisi tertulis pertama mengenai apa yang disebut sebagai rasio emas: "Sebuah garis dikatakan telah dipotong dalam rasio ekstrem dan rata-rata ketika panjang seluruh garis berbanding ruas panjang adalah sama dengan ruas panjang berbanding ruas pendek."^[5] Euclid menjelaskan cara memotong sebuah garis dalam "rasio ekstrem dan rata-rata", yaitu rasio emas.^[11] Di seluruh Element, beberapa pengajuan gagasan (teorema dalam istilah modern) serta pembuktiannya menggunakan rasio emas.^[12] Beberapa dari gagasan yang diajukan ini menunjukkan bahwa rasio emas adalah bilangan irasional.

Nama "rasio ekstrem dan rata-rata" adalah istilah utama yang digunakan pada abad ke-3 SM ^[5] hingga sekitar abad ke-18 M.

Sejarah modern rasio emas dimulai dengan karya Luca Pacioli De divina proportione pada tahun 1509, yang memukau para seniman, arsitek, ilmuwan, dan mistik dengan rumusan matematika dan sifat-sifat istimewa rasio emas.

Michael Maestlin, pertama kali menerbitkan perkiraan desimal rasio emas pada 1597.

Perkiraan inversi rasio emas dalam bentuk pecahan desimal, disebutkan bernilai "sekitar 0,6180340," pertama kali ditulis pada 1597 oleh Michael Maestlin dari Universitas Tübingen, dalam suratnya untuk mantan muridnya Johannes Kepler.^[13]

Sejak abad ke-20, rasio meas diwakili dengan huruf Yunani Φ atau φ (phi, berdasarkan nama Phidias, (pematung yang disebut-sebut menggunakan rasio ini) atau secara tidak lazim juga dilambangkan dengan τ (tau, huruf pertama untuk kata dalam Yunani kuno τομή yang berarti memotong.^[2]^[14]

Arif Ulaen

Buat Lencana Anda

Contact

arifchandraulaen.webnode

arifulaen@yahoo.co.id